量化策略-满仓梭哈

谢明亮

刚入交易坑的新手容易冲动，满仓一把梭就是干，毕竟市场时时刻刻的波动都是赤裸裸的诱惑。对这种靠“猜涨跌”为生的梭哈型短线选手，可以肯定的是，只要预测涨跌的胜率超过某个阈值，绝对有可能靠这招独步天下。那么，靠梭哈稳定盈利，究竟需要多大的胜率?这是个值得定量分析的问题。为简单起见，考虑以下量化策略:
（梭哈策略）：对某固定标的A，每日收盘前预测下一交易日收盘价较今日收盘价的涨跌幅 a .若a>0看涨则满仓买入，否则不操作。下个交易日收盘时不论盈亏一律清仓。每个交易日如此执行。若每次交易手续费率为 \varepsilon ，为让此策略年收益率达到 \alpha(\alpha>0) , 预测涨跌的成功率 p需满足什么条件?
在股价服从几何布朗运动(GBM)假设下，股价对数率回报率服从正态分布，即第 i 日的涨跌幅 a_i, b_i \sim N(\mu, \sigma^2). 先考虑 \mu=0 的情形，也就是纯粹的震荡行情. 那么第N 日受益的期望为
r_n = \Pi_{i=1}^N(1+|a_i|-\varepsilon)^p(1-|{b_i}|-\varepsilon)^{1-p}-1.
令 r_n \geq \alpha , 并取对数，得到
p \sum_i \log(1+|a_i|-\varepsilon) +   (1-p)\sum_i \log(1-|b_i|-\varepsilon) \geq \log(1+\alpha).
考虑大A股10%的涨跌幅限制 (a_i, b_i \in [-0.1, 0.1]) ，可以近似取上式左边的二阶泰勒展开
p \sum_i (|a_i|-\varepsilon-\frac{(|a_i|-\varepsilon)^2}{2}) + (1-p)\sum_i (-|b_i|-\varepsilon-\frac{(|b_i|+\varepsilon)^2}{2}) \geq\log(1+\alpha).
再对左边取期望. 根据正态分布假设， E[|a_i|] = \sqrt{\frac{2}{\pi}} \sigma, E[a_i^2] = \sigma^2. 带入得
(2p-1)(1+\varepsilon)\sqrt{\frac{2}{\pi}} \sigma - \frac{1}{2}\sigma^2 -\varepsilon\geq \frac{1}{N}\log(1+\alpha),
解得
p \geq \frac{1}{2} + \sqrt{\frac{\pi}{32}} \cdot \frac{\sigma}{1+\varepsilon} + \sqrt{\frac{\pi}{8}} \cdot \frac{\log(1+\alpha)+N\varepsilon}{N \sigma(1+\varepsilon)} \approx 0.5+0.31\sigma + \frac{0.63(\alpha+N\varepsilon)}{N\sigma}.
不难看出，当手续费 \varepsilon 足够小时对收益 \alpha 的影响完全是线性的。对主流券商，ETF买卖费差不多万二万三左右，不妨取交易一次的费率为 \varepsilon=0.0005 来计算。
先固定 \sigma ,考虑上证50, 近三年统计日波动率标准差 \sigma=0.016.


不难看出，涨跌幅分布基本符合正态分布假设。接下来我们看看在不同的 N  下，不同年收益率对应的梭哈胜率是多少(取)：


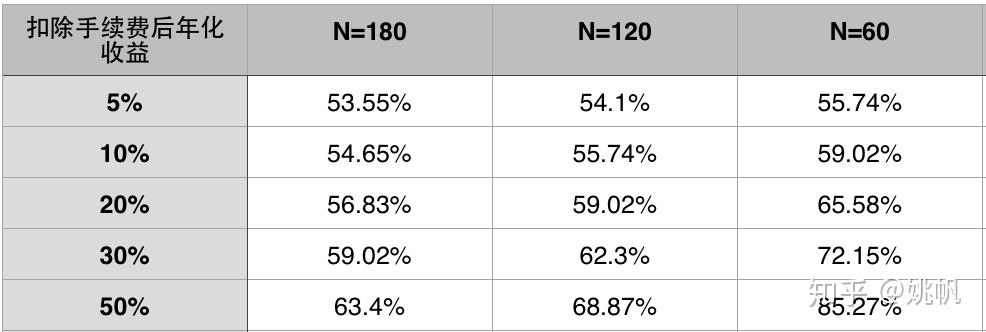
N 取小的好处是避免频繁交易，省手续费。而且显然 N 越小每次“梭哈”就越有把握，取得相应年化收益的最低准确率要求也就越高。
再固定 N=180, 即假设我们的“梭哈”策略对一年内近一半的交易日给出了买入指示. 对不同的波动率标的观察：


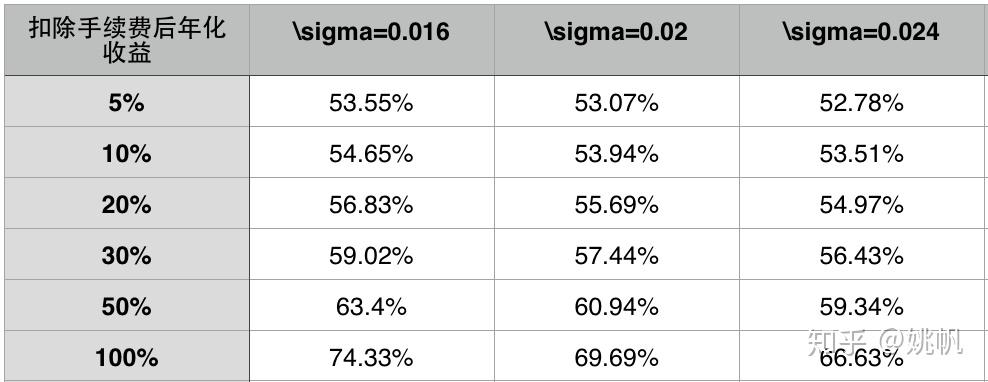
可以看到，在胜率超过一定阈值的情形下，标的波动率越高对总收益越有利。
综上我们可以近似总结出以下规律：

• “梭哈”取得正收益的预测成功率门槛大约在54%-55%左右。
  
• 只要策略成功率超过门槛，标的波动性对总收益贡献是正向的。
  
• 交易手续费对总收益的影响是线性且显著的。
  

如此看来，我们只需做到3点：

• 标的手续费低，例如免印花税的场内ETF.
  
• 标的波动大，如证券ETF，创业板指ETF.
  
• 搭建一个系统，最大化预测单日涨跌的准确率.
  

前两个都好说，怎么做第三点，下节继续讨论。

钱叔叔

大人，此事必有蹊跷！