第二章 消费者选择理论（6）：特殊偏好的案例

刀疤

6. 特殊偏好的案例

6.1 CES效用函数

齐次度为1的CES效用函数表达式为：
u(x,y)=(αx^ρ+βy^ρ )^{1/ρ},(α,β>0;ρ≤1,ρ≠0)   
先做对数变换（取对数属于单调变换），计算边际替代率会容易一些：
lnu=\frac{1}{ρ} ln⁡(αx^ρ+βy^ρ )


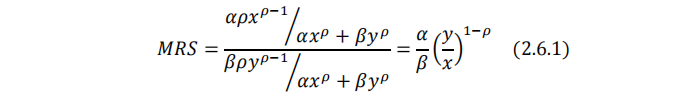
效用最大化的一阶条件为：


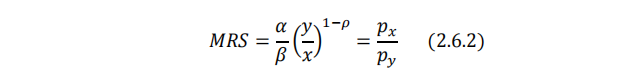
（2.6.2）式和预算约束（2.6.3）式联立：


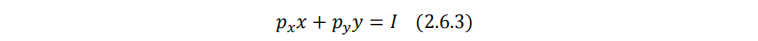
解得两种商品的马歇尔需求函数：


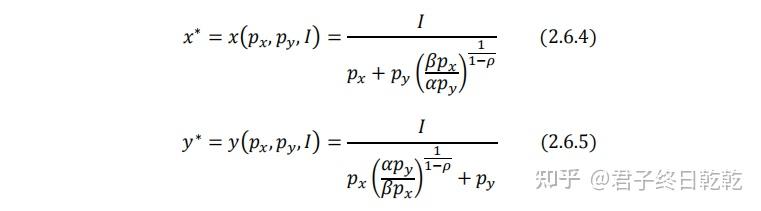
令参数 α=1,β=1 ，做必要的简化：
u(x,y)=(x^ρ+y^ρ )^{1/ρ}
这样就可以做形如 v(u)=u^ρ/ρ 的正单调变换了。新的效用函数形式为：


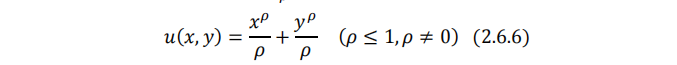
形如（2.6.6）式的效用函数被称为幂效用函数。当 ρ→0 时：


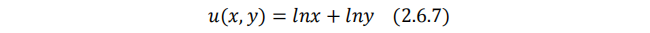
这实际上是参数为1/2的柯布-道格拉斯效用函数。读者可以自行证明。

截止到现在，我们还只是使用“不变替代弹性（CES）”的名称，却没有解释替代弹性（elasticity of substitution）的真实含义。替代弹性指相对价格上涨1%时，两种商品相对需求量变动的比例。它衡量了用一种商品替代另一种商品的难度：


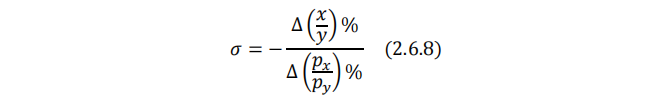
取负号是为了保持替代弹性为正。一般的弹性更强调绝对量之间的百分比变化关系，替代弹性则更强调相对量之间的百分比变化关系。
由于消费者均衡时， MRS=p_x/p_y  ，因此替代弹性公式也可以写作


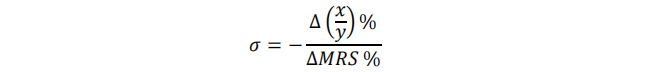
微分形式为：


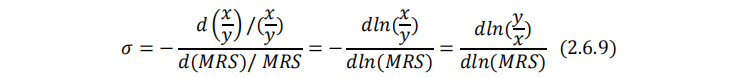
对于CES效用函数来说：


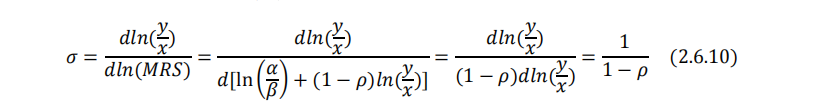
CES效用函数的替代弹性是一个不变量，且仅与参数 ρ 有关。
<hr/>6.2 柯布-道格拉斯偏好

CES效用函数虽然更具普遍性，但计算起来极为繁琐，我们就不进行更深入的计算了，转而讨论几个特例——这足以概括大多数情形了。
当 ρ →0时，CES效用函数为柯布-道格拉斯效用函数：
u(x,y)=x^α y^β     (α,β>0; α+β=1)
柯布-道格拉斯效用函数的替代弹性为1：
σ=\frac{1}{1-ρ}=1
代入（2.6.4）（2.6.5）式：


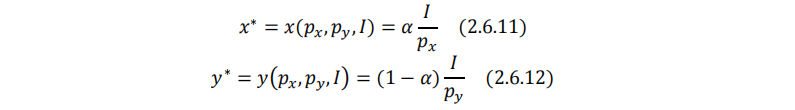
这表明了柯布-道格拉斯效用函数对应的马歇尔需求的一个性质：消费者在每种商品上的支出占收入的比例是固定的。换言之，消费者对每种商品的预算份额不变。


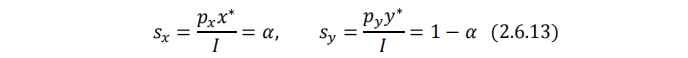
间接效用函数为：


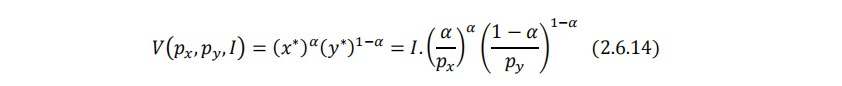
收入恒等于支出，且支出函数与间接效用函数互为反函数，故：


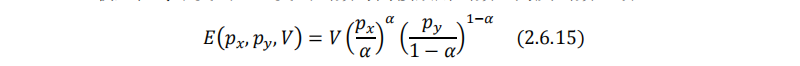
根据谢泼德引理，对支出函数（2.6.15）式求一阶偏导即希克斯需求函数：


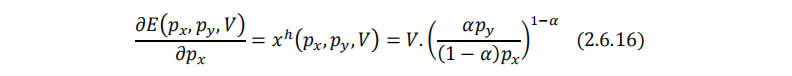
（这里只计算了商品x的相关数据，商品y的数据的计算方法与之一致，故而不再赘述。）
对希克斯需求函数（2.6.16）求一阶偏导数，即支出函数（2.6.15）式求二阶偏导数，可得替代效应：


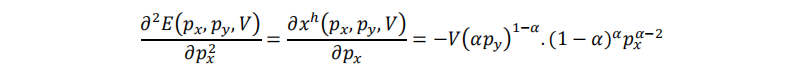
将（2.6.14）式代回：

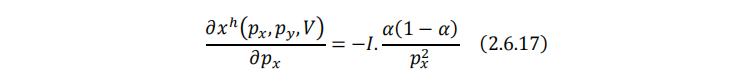
注：因为希克斯需求函数将间接效用视为一个不变常量，因此不能在求导之前代入（2.6.14）式。

（2.6.17）式就是柯布-道格拉斯效用函数对应的替代效应的表达式。
马歇尔需求函数（2.6.11）式对价格 p_x 求偏导可得总效应：


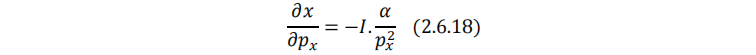
收入效应的表达式为：


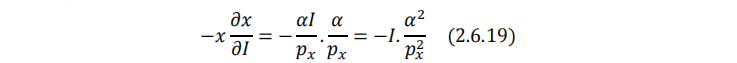
（2.6.17）（2.6.18）（2.6.19）三式联立，可验证斯勒茨基方程：


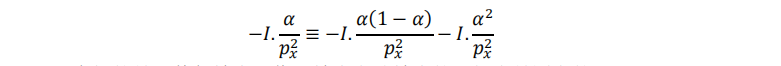
有趣的是，替代效应和收入效应占总效应的比例也是固定的：


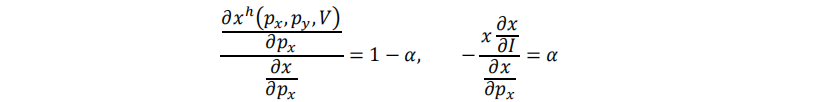
还可以计算各类弹性：


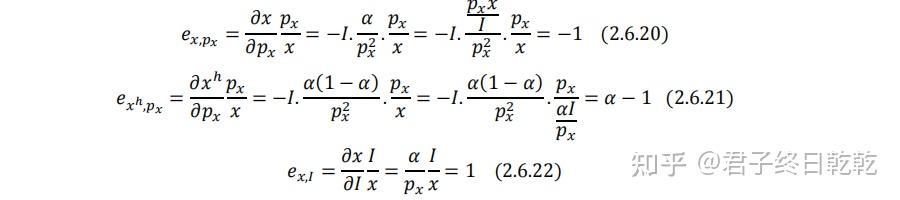
这时就显示出弹性形式的斯勒茨基方程的优势了：


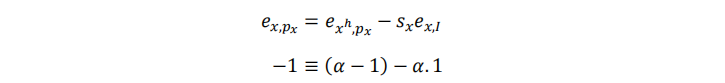
柯布-道格拉斯偏好的交叉总效应（从而交叉需求弹性）为0。


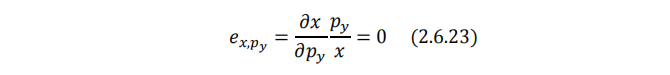
但这绝不意味着柯布-道格拉斯偏好下商品x和商品y无关。为了看清这一点，我们需要借助于斯勒茨基方程。其中，（2.6.16）式对 p_y 求导可得希克斯交叉替代效应：


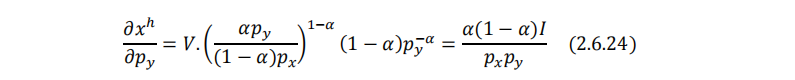
收入效应：


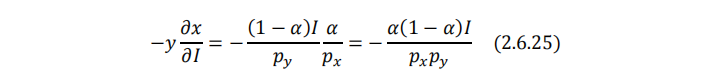
换言之，柯布-道格拉斯偏好的交叉总效应为0，纯粹是凑巧——替代效应和收入效应互相抵消了。这时，商品x和商品y既不算总替代品，也不算总互补品，但一定互为净替代品。
<hr/>6.3 完全替代型偏好

当 ρ=1 时，CES效用函数为完全替代型效用函数：
u(x,y)=αx+βy,(α,β>0)
此时替代弹性为无穷大：
σ=1/(1-ρ)=∞
这个效用最大化问题只存在角点解。求（2.6.4）（2.6.5）式在 ρ→1 时的极限：
也就是说，当预算线比无差异曲线更缓时，消费者会将全部收入用来消费商品x；当预算线比无差异曲线更陡时，消费者会将全部收入用来消费商品y。
（当预算线和无差异曲线重合时消费者可以消费预算线上任一点，我们暂时不考虑这种情况。）




间接效用函数为：


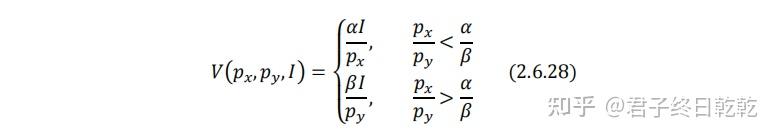
支出函数与间接效用函数互为反函数：


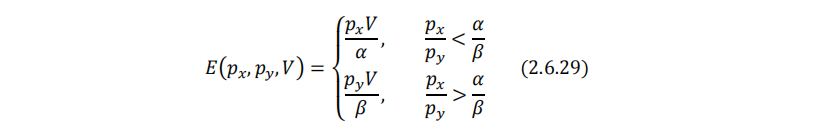
希克斯需求函数为：


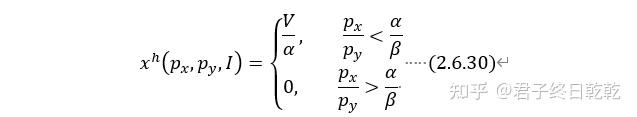
下面我们要针对不同情况，对完全替代偏好下的斯勒茨基方程展开讨论。
（I） p_x 变动前后都是 p_x/p_y <α/β ：
很显然，角点解没有变化，仍然是 x=I/p_x  ，没有发生任何“替代”。因此，价格变化的总效应被完全归因于收入效应。数学运算也支持我们的分析：
总效应：
\frac{∂x}{∂p_x }=-\frac{I}{p_x^2 }
收入效应：
-x \frac{∂x}{∂I}=-\frac{I}{p_x} \frac{1}{p_x} =-\frac{I}{p_x^2}
替代效应：
\frac{∂x^h}{∂p_x}=0
（II） p_x 变动前后都是  p_x/p_y >α/β ：此时商品x的需求保持为0，没有什么分析的必要。对于商品y的分析，请参见（I）。
（III） p_x 变动前是 p_x/p_y <α/β ，变动后是 p_x/p_y >α/β ：
有一点是明确的：消费者不会在两种商品中进行权衡，而是“梭哈”——要么全买，要么不买。因此，消费者实现了两种商品的“完全替代”——价格变化的总效应被完全归因于替代效应。
这时候，导数方法就不适用了——因为商品x的需求函数不连续。但最原始的变动值的斯勒茨基方程还是可以使用的：
∆x≡∆x^s+∆x^n


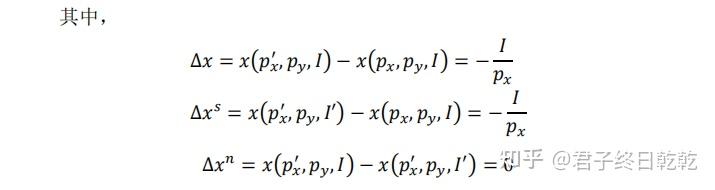
p_x'  表示变动后商品x的价格。
<hr/>6.4 完全互补型偏好

当 ρ→-∞ 时，CES效用函数为完全互补型效用函数：
u(x,y)=min⁡(αx,βy)
和完全替代型不同，完全互补型的效用最大化问题是有内点解的——但是同样不能用拉格朗日方法求解，因为效用函数不可导。
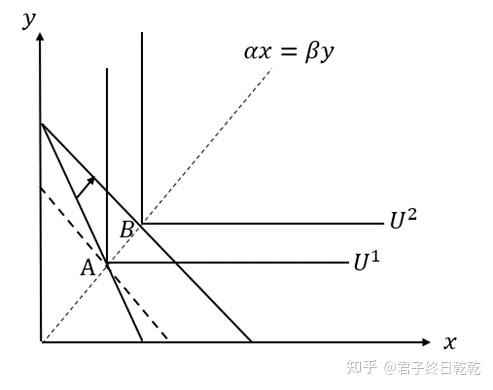
做图可知，消费者均衡出现在无差异曲线的直角拐点处。故效用最大化条件为：
αx=βy
代入预算约束当中求解需求函数（对（2.6.4）（2.6.5）式求极限的结果与之相似）：


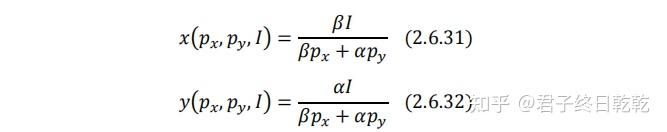
两种商品的间接效用函数为：


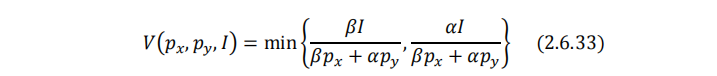
支出函数为：


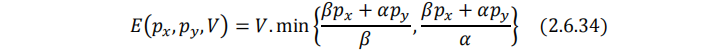
这个函数不可导。很显然，完全互补型偏好不存在一个连续的希克斯需求函数，更不存在替代效应。
从下图来看，相对价格变化后，补偿预算线对应的最优选择仍然是A点。这说明，替代效应为0，相对价格变化的总效应被完全归因于收入效应。


使用变动值的斯勒茨基方程：
∆x≡∆x^s+∆x^n
其中，


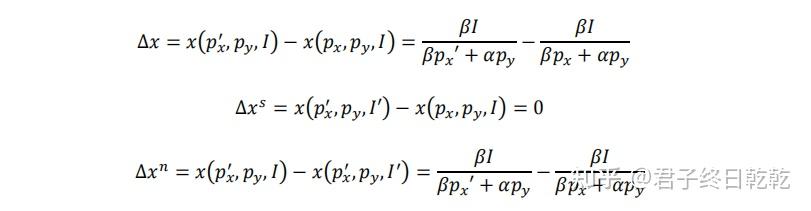
<hr/>6.5 拟线性偏好

拟线性偏好对应的效用函数形式为：


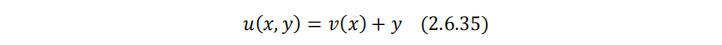
效用函数对商品y来说是线性的，但对商品x来说是非线性的，因此称为拟线性（quasi-linear）。
对于拟线性偏好而言，效用最大化的一阶条件为：


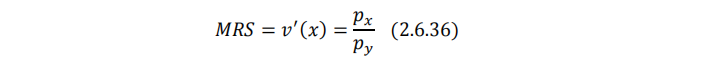
显然，拟线性偏好是非位似的，因为它和 y/x 无关。
一个良态偏好首先要满足单调性和边际替代率递减规律，因此：
v' (x)>0,v''(x)<0
从（2.6.36）式可以求出商品x的马歇尔需求函数，记为


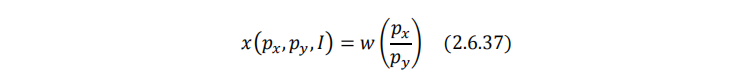
函数 w(.) 是 v' (x) 的反函数。很显然，商品x的马歇尔需求只与相对价格 p_x/p_y  有关。为了简化计算，我们设 p=p_x,p_y=1 。故 v' (x)=p  。
从而商品y的马歇尔需求函数为：


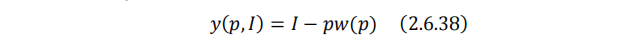
请注意，某种商品的需求量一定是非负的。这里我们必须考虑这一点。故：
I≥pw(p)
因此，消费者的收入必须足够多，否则他不会消费商品y。如果收入不足，消费者就会将全部收入用来消费商品x。若 I<pw(p) ，马歇尔需求函数是：


一般我们不考虑这种情况，而假设收入是足够大的。进而有间接效用函数：


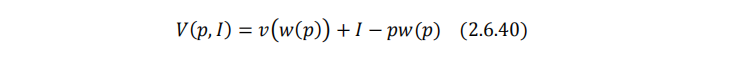
支出函数：


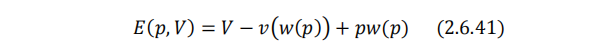
对p求导，计算希克斯需求：


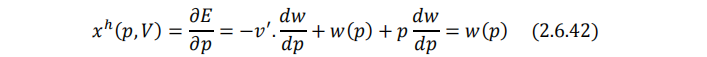
这表明，拟线性偏好对应的马歇尔需求和希克斯需求恒等（对于商品x）。因此，价格变动的总效应被全部归因于替代效应，收入效应等于0（马歇尔需求函数只与相对价格p有关而与收入I无关，自然没有收入效应）。
从图形上看，拟线性偏好的特点是这样的：


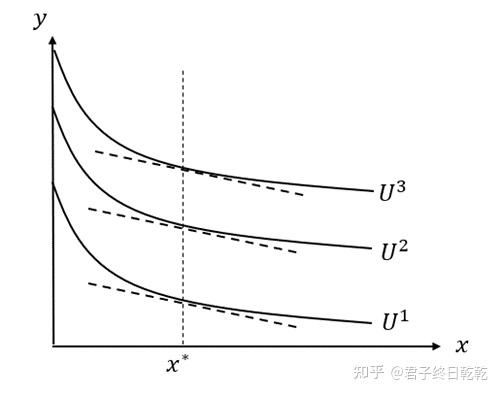
因为没有收入效应，所以收入的变化（也就是预算线的平移）不会影响消费者对商品x的最优选择。很显然，两条预算线之间的垂直距离等于两条拟线性无差异曲线之间的垂直距离。
我们会在什么情况下使用拟线性偏好呢？答案是：商品x是研究者关心的商品，而商品y则被抽象为以货币计价的“所有其他商品”（又称复合商品）。因此“商品y”的价格为1（1单位货币的价格当然是1）。这为我们前面计算时将价格简化为 p_y=1 又提供了一个理由。
很显然，拟线性偏好下的商品x具有这样的特点：当收入较少时，消费者可能会将全部收入用来消费它；而随着收入的上升，消费者对这种商品的需求不再增长。食品、盐等生活必需品具有这样的特点。
<hr/>前情提要：
点击下方链接，欢迎咨询购书（微观经济学、宏观经济学、微观经济学数理分析）、经济学考研等事宜。
初级经济学请关注：